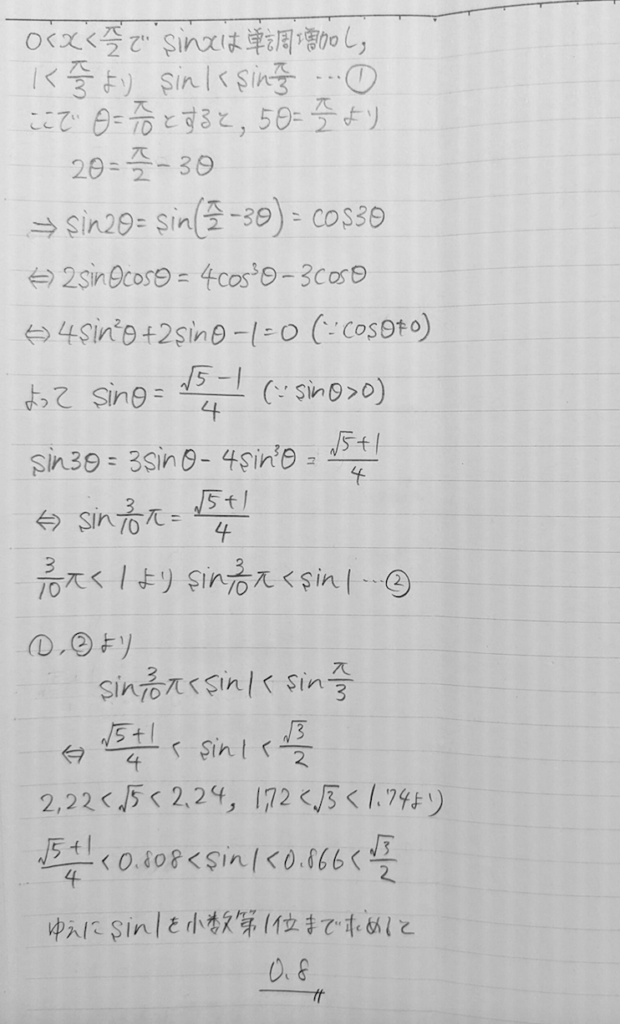はじめまして! 釧路湿原大学運営のユルリ島です。当サイトでは主に高校数学、理科、地理、情報等に関する記事をあげていく予定ですが、今回は数学の第1回として自作の問題を解説していきます(既出の問題でしたらすみません)。今後は不定期で自作問題や典型問題の解説、および入試問題の解説等を行っていく予定ですのでどうぞよろしくお願いします。
それでは早速始めていきましょう!
$\fbox{1}\ \ \sin1の値を小数第1位まで求めよ。$
第1回は三角関数を扱います。誰でも思いつきそうななんとも単純な問題ですが、解説を始めていきます笑。京都大学の某問題に見た目が似ている気もする。
まず、$\sin1$なんて値は勿論そのまま出せないですし、$π$が絡んだ数でもないので倍角の公式を使い導くこともできません。よって、不等式で評価をする方針でいきましょう。有名角の$\sin$で挟みたいので1に近い有名角を探していきます。まず初めに思いつくのは$\frac{π}{3}$でしょうか、これは1よりも少し大きい値ですので上から挟むことはできそうです。下からの評価は少し思いつきにくいですが$\frac{3}{10}π$で評価できると推測し、倍角の公式を用いてこの値を求めていきます。$\frac{1}{10}π$系統の三角比の問題を解いたことがある人は簡単に思いついたかもしれませんね。
解答
$0<x<\frac{\pi}{2}$で、$\sin x$は単調増加し、
$1<\frac{\pi}{3}$より、
$$\sin 1<\sin\frac{\pi}{3} \tag{1}$$
ここで、$\theta=\frac{\pi}{10}$とすると、$5\theta =\frac{\pi}{2}$より、
$$
\begin{aligned}
&2\theta =\frac{\pi}{2}-3\theta\\
\Longrightarrow&\sin 2\theta=\sin(\frac{\pi}{2}-3\theta)=\cos 3\theta\\
\Longleftrightarrow&2\sin\theta\cos\theta=4\cos^3\theta-3\cos\theta\\
\Longleftrightarrow&4\sin^2\theta+2\sin\theta-1=0\qquad(\because\sin\theta\ne0)
\end{aligned}
$$
よって、$\sin\theta=\frac{\sqrt{5}-1}{4}\quad(\because\sin\theta>0)$
$$
\sin3\theta=3\sin\theta-4\sin^3\theta=\frac{\sqrt{5}-1}{4}\\
\Longleftrightarrow\sin\frac{3}{10}\pi<\sin1
$$
$\frac{3}{10}\pi<1$より、
$$\sin\frac{3}{10}\pi<\sin1 \tag{2}$$
$(1)(2)$より、
$$
\sin\frac{3}{10}\pi<\sin1<\sin\frac{\pi}{3}\\
\Longleftrightarrow\frac{\sqrt{5}-1}{4}<\sin1<\frac{\sqrt{3}}{2}
$$
$2.22<\sqrt5<2.24$、$1.72<\sqrt3<1.74$より、
$$\frac{\sqrt{5}-1}{4}<0.808<\sin1<0.866<\frac{\sqrt3}{2}$$
ゆえに、$\sin1$を小数第一位まで求めると、
$$0.8$$