【高校数学Ⅰ】2次関数のグラフをマスターしよう！

今回から高校数学の中で最初の難関でもある二次関数について解説していきます！基礎から応用まで幅広く扱っていく予定なので数学で苦手な分野がある時や、数学力を高めたい時に是非ご覧ください。

関数とは？

ある変数$\ x\ $があるとき，この$\ x\ $を関数という箱にいれると$\ y \ $の値がただ1つに決まる時$\ y\ $は$\ x\ $の関数といいます。関数は$\ f(x)\ $ と表し，ある関数$\ f\ $ に$\ x\ $を代入していることを表しています。下図のようなイメージですね。

　　　　　　　　　　　　　　$x$➡︎$f$という関数➡︎$f(x)$として値が出てくる

また関数$ y=f(x) $において$ x=a $のときの$ y $の値を$ f(a) $と表します。
例えば$ f(x)=x+3 $のとき$ x=2 $のときの$ y $の値は$ f(2)=2+3=5 $といった具合です。

象限

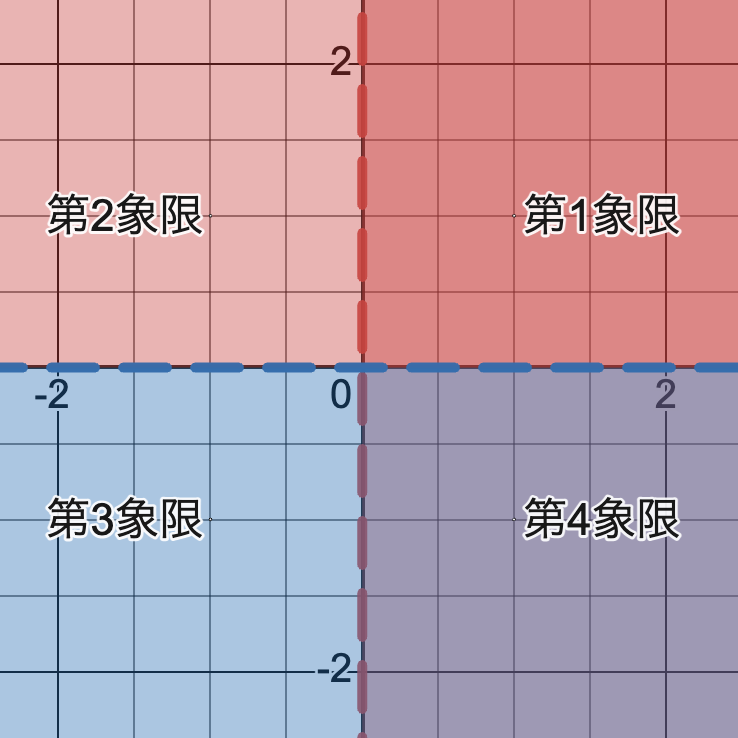
座標平面には$ x$軸と$ y$軸の2つの軸があります。この2つの$ x$軸と$ y$軸で平面が4つに分割されるとき，この分割された4つの領域を第1象限から第4象限までで分類します。どこが題2象限であるか〜などは覚える必要があります。下図のようになるので覚えましょう。また$ x軸$や$ y$軸上の点はどの象限にも含まれないので注意しましょう。

2次関数のグラフ・軸・頂点

2次関数のグラフは放物線と呼ばれ， $y=ax^2+bx+c$ (一般形)の形で表されます($a≠0$)。
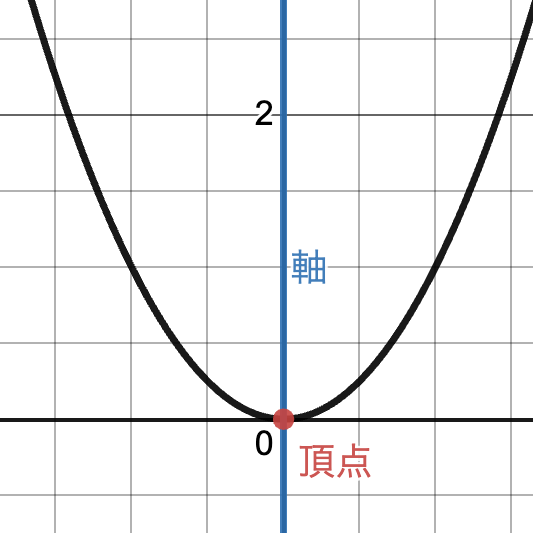
また放物線に関わる重要な言葉として，軸と頂点があります。
軸とは…放物線はある直線を境に線対称な図形になっています。この直線を軸といいます。
頂点とは…放物線とその軸の交点のことを頂点といいます。

2次関数の形は $a$ の値により大きく変わります。

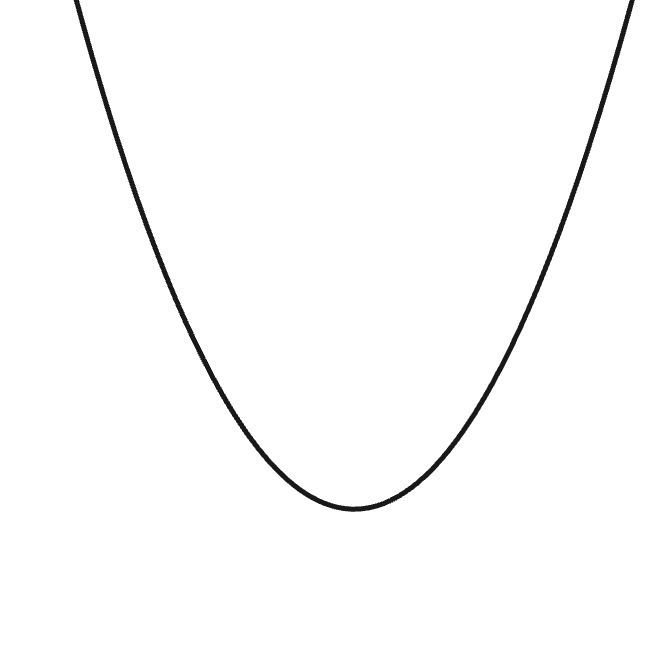
(1) $a>0$ のとき，
　 放物線のグラフは下に尖った形となり，これを下に凸(したにとつ)と呼びます。

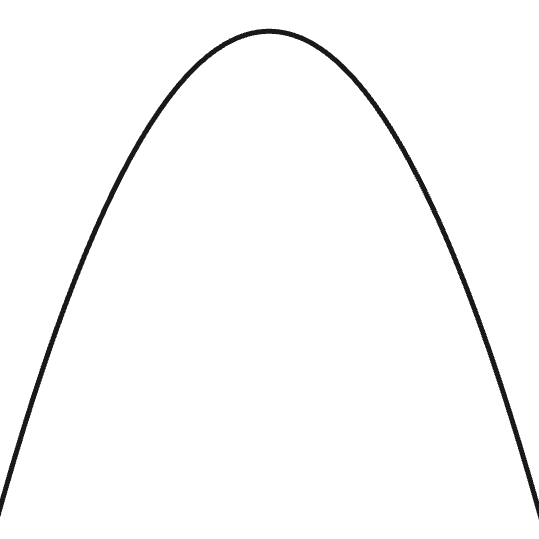
(2) $a<0$ のとき，
　 放物線のグラフは上に尖った形となり，これを上に凸(うえにとつ)と呼びます。

$y=a(x-p)^2+q$(標準形)のグラフと平方完成

$y=ax^2+bx+c$ の表記ではグラフをかくことは難しいです。しかし，グラフの頂点と軸が分かればグラフの概形をかくことができます。2次関数を $y=a(x-p)^2+q$(標準形) の形に変形することでグラフの頂点と軸を知ることができます(理由は後程説明)。この変形を平方完成といいます。

・平方完成のやり方
$y=ax^2+bx+c$

$=a(x^2+\frac{b}{a}x)+c$

$=a{(x+\frac{b}{2a})^2-(\frac{a}{2b})^2}+c$

$=a(x+\frac{a}{2b})^2-\frac{b^2}{4a}+c$

ここで，$p=-\frac{a}{2b} ， q=-\frac{b^2}{4a}+c$ とおくと

$y=a(x-p)^2+q$ を得る。■

平方完成は慣れなので数を沢山こなしましょう。

・標準形から軸と頂点を求める。

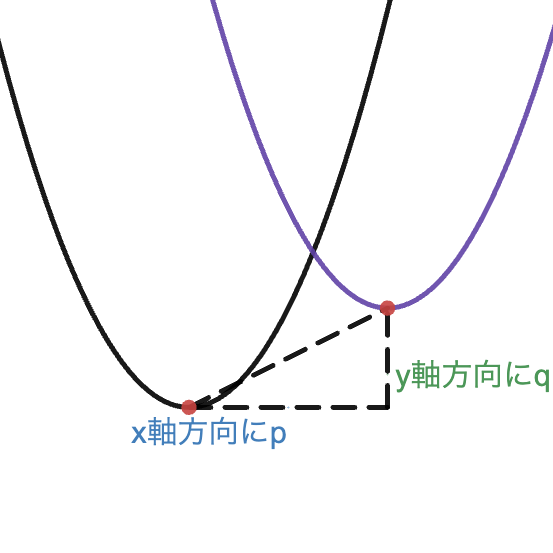
$y=a(x-p)^2+q ⇔ y-q=a(x-p)^2$ は $y=ax^2$ の $x$ を $x-p$，$y$ を $y-q$ に置き換えた形をしています。この変換は $y=ax^2$ のグラフを $x$ 軸方向に $p$ ，$y$ 軸方向に $q$ だけ平行移動させたグラフを表しています。

$y=ax^2$ の軸は $x=0$ なので，$x$ 軸方向に $p$ 平行移動させた $y=a(x-p)^2+q$ の軸は $x=p$
同様に，$y=ax^2$ の頂点は $(0,0)$ なので，$x$ 軸方向に $p$ $y$ 軸方向に $q$ 平行移動させた $y=a(x-p)^2+q$ 頂点の座標は$(p,q)$ となります。

定義域・値域・最大値・最小値

関数 $y=f(x)$ において，$x$ の取りうる範囲を定義域，そのときの $y$ の取りうる範囲を値域といいます。また，値域のうち最も大きい値があるとき，その値を最大値，逆に値域のうち最も小さな値があるとき，その値を最小値と言います。

〈例1〉 $y=2x$ の定義域が$ -1<x≦3 $のときの値域・最大値・最小値は?

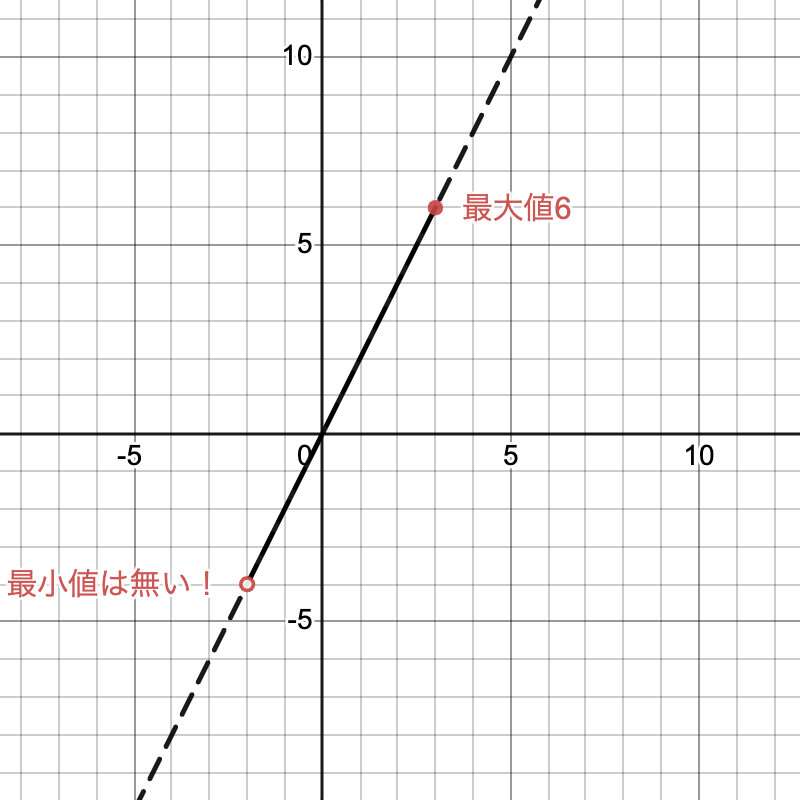
$y=2x$ は直線を表すので，端点を考えると値域は $-2<y≦6$ となります。
よって最大値は6となります。一方最小値は，値域の不等式に左側に等号(=)が含まれないので最小値はありません。

〈例2〉

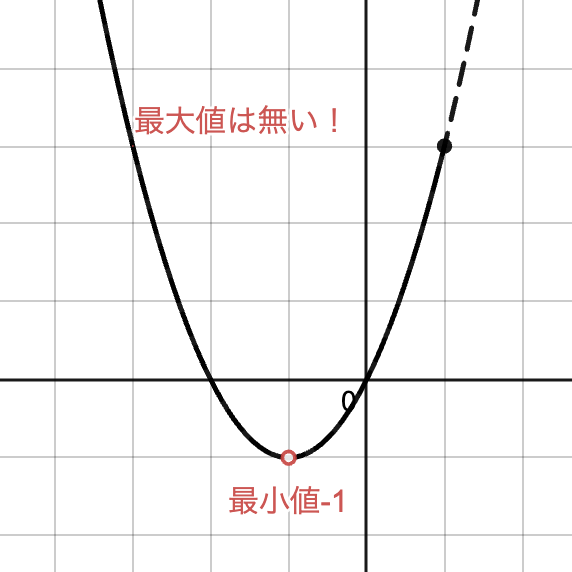
$y=x^2+2x$ の定義域が $x≦1$ のときの値域・最大値・最小値は?

2次関数なのでグラフの形を考えましょう。平方完成すると $y=(x+1)^2-1$ となり，軸は $x=-1$ ，頂点は$ (-1,-1)$ であることがわかります。グラフをかくと，最小値は $x=0$ のとき$0 $ですが，$ x $の定義域が負の方向に無限に続くので最大値は存在しません。

〈例3〉

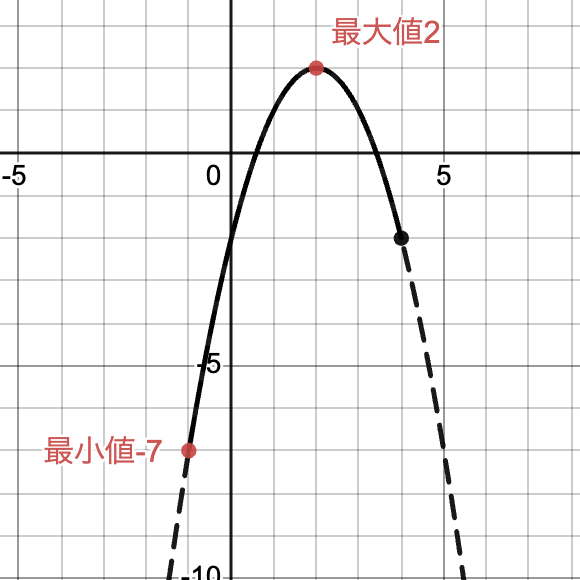
$y=-x^2+4x+1$ の定義域が $-1≦x≦4$ のときの最大値と最小値は?

これも2次関数なので平方完成すると，$y=-(x-2)^2+2$ となり頂点の座標が$ (2,2)$ とわかります。 $x^2$ の係数が負であるので上に凸であることに注意すると，グラフは以下のようになります。よって最大値は $x=2$ のとき$2$，最小値は $x=-1$ のとき $-7$ となります。

第1回は2次関数の基本事項について整理しました。次回からは2次関数の頻出問題や応用問題の解説をしていきますのでよろしくお願いします。なお，記事に誤りがありましたらご気軽にコメントください。最後に練習問題を載せておきますので力試しにどうぞ！

以下解答⇩